Geometria

                          Geometría  

Indice: 

1El triángulo
2. Lugares geométricos
3. Movimientos en el plano
4. Resumen de áreas y volúmenes de figuras conocidas
5. La esfera y el globo terráqueo
6. Bibliografía
SOFTWARE: Geogebra http://www.geogebra.org/webstart/geogebra.html


                                                             1. El triángulo

1.1 Propiedades y tipos de triángulos


Triángulo equilátero 

•  Tres lados iguales.

Triángulo Isósceles

       

•         Dos lados iguales.

Triángulo escaleno 

• Tres lados desiguales.

TIPOS DE TRIÁNGULOS (Según sus ángulos).

Triángulo acutángulo 

• Tres ángulos agudos.

Triángulo rectángulo

• Un ángulo recto.(El lado mayor es la hipotenusa).
  Los lados menores son los catetos

Triángulo Obtusángulo

• Un ángulo Obtuso.

1.2 Rectas y puntos notables en el triángulo.

(http://gaussianos.com/los-centros-del-triangulo-incentro-baricentro-circuncentro-y-ortocentro/)

En el triangulo equilátero coinciden todas las rectas y puntos notables  tratados, es decir, las medianas, las alturas, las bisectrices y las mediatrices, así como el baricentro, el
ortocentro, el incentro y el circuncenro. En el triángulo isósceles la altura relativa a la base, es mediana, bisectriz y mediatriz.

1.3 El teorema de Pitágoras

El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos. Es la proposición más conocida entre las que tienen nombre propio en la matemática.

1.3.1 Demostración gráfica.

(http://gaussianos.com/lo-que-se-puede-hacer-con-geogebra-ix-
demostracion-visual-del-teorema-de-pitagoras/)

 
1.3.2 El teorema en 3D

 
1.4 El teorema de Tales (vídeo: Les Luthiers - Teorema De Thales.

(https://www.youtube.com/watch?v=UbalEyegXbQ), triángulos semejantes. ¿Cómo calcular
la altura de un árbol a partir de su sombra?

Trazando imaginariamente un triángulo entre el objeto a medir y su sombra y usando el Teorema de Pitágoras, el cual establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto o L).

 

 

                           2. Lugares geométricos

2.1 ¿Qué es un lugar geométrico?

Se denomina lugar geométrico al conjunto de los puntos del plano que satisfacen una determinada propiedad. Dicha propiedad se enuncia habitualmente en términos de distancias a puntos, rectas o circunferencias fijas en el plano y/o en términos del valor de un ángulo.

2.2 La mediatriz y la bisectriz

 
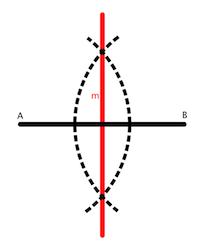
       Mediatriz: Lugar geométrico de los puntos del plano que                    equidistan  de los extremos de un segmento.







 

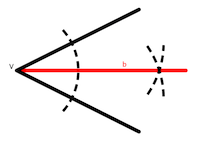
Bisectriz:Lugar geométrico de los puntos del plano que equidistan de las semirrectas que forman el ángulo


 



2.3 Las cónicas /2.3.1 ¿Qué es una cónica?   


Se denomina sección conica a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas  propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

 2.3.2 La circunferencia 


   

La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro. Una circunferencia  es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo llamado centro.

2.3.3 La elipse:


La elipse es una curva plana, simple y cerrada. La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante.

• Obtención en un cono

• Método del jardinero

• Mesa de billar elíptica

 

Animación: http://centros5.pntic.mec.es/ies.victoria.kent/Rincon-C/Simulaci/b-e/b-e.htm
Vídeo del hormiguero: http://www.antena3.com/videos-online/programas/el-
hormiguero/secciones/ciencia-marron/billar-infalible_2011100600179.html


2.3.4 La hipérbola

• Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.

• Obtención en un cono La lámpara hiperbólica

• Muchos tienen en sus casas esas lámparas con pantalla  que se usan en los living-rooms o en la mesas de luz de las habitaciones, que al estar encendidas emanan un cono de luz hacia arriba y otro hacia abajo, los cuales forman sobre la pared dos  figuras con forma de hipérbole.

 

2.3.5 La parábola 

En matematicas , una parábola es la sección cónica de excentricidad igual a 1,resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.

• Obtención en un cono  La antena parabólica  El horno solar

El horno solar:
El Horno Solar Parabólico es un instrumento que permite cocinar alimentos empleando exclusivamente la el poder calorífico del sol. El funcionamiento de este ingenio es sencillo. 1º

 
 
 
3.2 Ejercicios de vectores y translación
3.2.1 Dados los vectores u=(4,3) y v=(-1,4), hallar:

a) su representación gráfica en un sistema de coordenadas
b) los vectores u + v y u - v por la regla del paralelogramo.=3.7
c) las componentes de los vectores anteriores
d) el módulo de cada uno de los vectores.

3.2.2 Dibuja las figuras trasladadas de las siguientes en una traslación de vector guía u(4,3):
 
3.3 Giros
3.3.1 Ejercicio: Escribe la inicial de tu nombre y haz varios giros con ella.
3.4 Simetría. Ejercicios
3.4.1 Dado el triángulo de vértices A(-2,2), B(6,-1) y C(7,5) se pide:
a) dibujar el triángulo
b) hallar el triángulo simétrico respecto del centro de simetría O(0,0)
c) hallar el triángulo simétrico respecto del eje OX
 3.4.2 Euclides (aproximadamente 300 a. C.) enunció lasleyes de reflexión de la luz sobre un espejo plano.Herón de Alejandría, 400 años después, afirmóalgo más sencillo: "La luz ha de tomar siempre el camino más corto". Sirviéndote de esta idea,halla en que punto del espejo se ha de reflejar un rayo de luz que parte del punto A para que después llegue a B.
A B M Espejo.
3.4.3 Carlos y Fernando están jugando al billar. En un determinado momento las bolas se encuentran en las posiciones indicadas por el dibujo. Indica el camino que debe seguir la bola A para que rebotando en la banda MQ golpee a la bola B. 



 4. Resumen de áreas y volúmenes de figuras conocidas.

 

 

5. La esfera y el globo terráqueo
5.1 Elementos principales de la esfera.
5.2 Elementos de la esfera terrestre.
5.3 Los husos horarios, la hora local solar y oficial.
5.4 El método de Eratóstenes para calcular el diámetro de la circunferencia terrestre.

 

 
Centro: Punto interior que equidista de cualquier punto de la esfera.
Radio: Distancia del centro a un punto de la esfera.
Cuerda: Segmento que une dos puntos de la superficie.
Diámetro: Cuerda que pasa por el centro.
Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.




Un globo terráqueo es un modelo a escala tridimensional de la Tierra, siendo la única representación geográfica que no sufre distorsión. Si bien la Tierra es el planeta más frecuentemente representado, existen modelos del Sol, la Luna y otros planetas, incluyendo algunos ficticios.
Los globos terráqueos suelen montarse en un soporte en ángulo, lo que los hace más fáciles de usar, representando al mismo tiempo el ángulo del planeta en relación al Sol y a su propio giro. Esto permite visualizar fácilmente cómo cambian los días y las estaciones.
Un globo terráqueo tiene a veces relieve, mostrando la topografía. Se suele usar una escala exagerada para el relieve, de forma que resulte visible.
La mayor parte de los globos terráqueos modernos incluyen también paralelos y meridianos, de modo que se pueda localizar una ubicación en la superficie del planeta.Eratóstenes inventó y empleó un método trigonométrico, además de las nociones de latitud y longitud, al parecer ya introducidas por Dicearco para medir la circunferencia de la Tierra.
Por referencias obtenidas de un papiro de su biblioteca, sabía que en Siena (hoy Asuán, Egipto) el día del solsticio de verano los objetos verticales no proyectaban sombra alguna y la luz alumbraba el fondo de los pozos; esto significaba que la ciudad estaba situada justamente sobre la línea del trópico y su latitud era igual a la de la eclíptica que ya conocía.  
 
Sagan https://www.youtube.com/watch?v=4gpECWx8sns)