1 PARTE: Conceptos básicos
1. ¿Cómo puedes expresar la relación entre dos magnitudes como, por ejemplo, la masa y el volumen de un cuerpo?
Una de las propiedades físicas intensivas de la materia es la densidad que relaciona directamente proporcional la masa de una sustancia con el volumen que esta ocupa.
2. ¿Qué es una función? ¿De qué formas pueden expresarse las relaciones entre magnitudes? Pon ejemplos de funciones de la vida cotidiana; puedes buscar en revistas, periódicos, etc. En las figuras siguientes tienes 3 ejemplos:
En análisis matemático, el concepto general de función, aplicación o mapeo se refiere a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero)se pueden expresar mediante tablas, gráfica, ecuaciones o formulas.
En geometría analítica, puede referirse a la pendiente de la ecuación de una recta(o coeficiente angular ) como caso particular de la tangente a una curva , en cuyo caso representa la derivada de la función en el punto considerado, y es un parámetro relevante, por ejemplo, en el trazado altimétrico de carreteras, vías ...
Primer ejemplo:Es una pendiente decreciente.(foto)
Medida de la inclinación de una línea que muestra que la línea baja de izquierda a derecha. Por ejemplo, y = -x + 2 tiene una pendiente de - 1.
Segundo ejemplo: Es una pendiente decreciente. Medida de la inclinación de una línea que muestra cómo sube de izquierda a derecha. Por ejemplo, y = x + 2 tiene una pendiente de 1.
3 . ¿Qué es la tasa de variación de una función? ¿Qué valores toma para las funciones crecientes y decrecientes? Puedes utilizar ejemplos gráficos para responder.
Es el incremento de una función, que mide lo que cambia al pasar de un punto a otro. En las crecientes, toma un valor superior a 0 (positivo), y, en las decrecientes, toma un valor menor a 0 (negativo)
4. Utilizando la representación gráfica de una o varias funciones, explica las diferencias entre máximos y mínimos absolutos y relativos.
El mínimo relativo en una función (F) es el punto donde la variable de evalúa que toma el valor más bajo en un Intervalo determinado, mientras que el mínimo absoluto es el punto donde la variable de toma que evalúa el valor más Bajo independientemente del Intervalo.
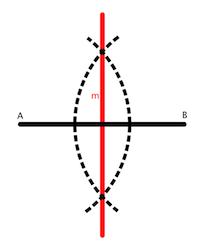
5. Representa gráficamente dos ejemplos de funciones simétricas respecto al eje de ordenadas (eje y) y respecto al origen (0,0). Explica en qué consiste cada tipo de simetría.
- Eje (y) y respecto al origen (0,0)
- Esto es una función simétrica impar que pasa por el eje (0)
Una función (f) es simétrica si al doblar su gráfica por un eje de simetría ésta se superpone.
Esto es una función simétrica par que pasa por el eje(0).
Desde un punto de vista geométrico, una función par es simétrica con respecto al eje y, lo que quiere decir que su gráfica no se altera luego de una reflexión sobre el eje y.
6. Representa gráficamente una función periódica indicando por qué se denomina de esa forma.

Función que repite el mismo valor a intervalos regulares de la variable. Una función f(x) es periódica si existe un número (p) tal que pueda hacer f (x+p) = f(x) para todas las (x). Al menor número (p) se le llama período
Osea es una función que repite todo el rato lo mismo .
7. Pon dos ejemplos, uno de función continua y otro de función discontinua. ¿Cuál es la diferencia entre ambas?
- Función continua . ... Si la función no es continua , se dice que es discontinua. Una funcion continua de en es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel (más formalmente su grafo es un conjunto conexo).
- Una función presenta discontinuidad evitable en un punto a, si tiene límite en un punto, pero la función en ese punto tiene un valor distinto o no existe, veamos estos dos casos. Si el límite cuando x tiende a a, es c, y el valor de la función evaluada en a es d, la función es discontinua en a.
Diferencia
Una función es continua si su gráfica puede dibujarse de un solo trazo, osea si puede dibujarse sin separar el lápiz de la hoja de papel. Y la función discontinua, es la que presenta algún punto en el que existe un salto y la gráfica se rompe.
8. Investiga: ¿Cuál es el origen del término función?
No apareció hasta los inicios del cálculo en el siglo XVII. René Descartes, Isaac Newton y Gottfried Leibniz establecieron la idea de función como dependencia entre dos cantidades variables. Leibniz en particular acuñó los términos «función», «variable», «constante» y «parámetro». La notación f(x) fue utilizada por primera vez por A.C. Clairaut, y por Leonhard Euler en su obra Commentari de San Petersburgo en 1736.
2 PARTE: Estudio y representación de funciones
9. Representa gráficamente las funciones que se proponen indicando sus propiedades. Elabora una tabla resumen con todas las gráficas obtenidas.
Funcion lineal creciente →→→
Función lineal constante →→→
Función lineal decreciente →→→

Rectas paralelas →→→→→→
Rectas perpendiculares →→→→→→
Rectas secantes →→→→→→
Función cuadrática cóncava →→→
Función cuadrática convexa →→→
Función cuadrática →→→→→→→

Función racional →→→→→→→
Función irracional →→→→→→→
Función exponencial →→→→→→→
Función logarítmica →→→→→→→

Función afín →→→→→→→

Función periódica →→→→→→→

Función discontinua →→→→→→→

Función afín normal →→→→→→→
Función proporcionable →→→→→→→
10. Investiga sobre la representación de funciones en coordenadas polares.
Las coordenadas polares o sistemas polares son un sistema de coordenadas bidimensional en el que cada punto del plano se determina por una distancia y un ángulo.
11.Utilizando uno de los programas anteriores investiga sobre la representación gráfica de
funciones en el espacio (x, y, z).
12.Utiliza el programa que has elegido para resolver gráficamente el sistema de dos ecuaciones lineales con dos incógnitas siguiente:
3x-2y=4
2x+3y=33
Resultado: 6.7
13.Elige un modelo de coche que disponga de motorizaciones Diesel y gasolina y realiza un estudio gráfico de la función coste que nos permita averiguar cual es el automóvil más adecuado para nosotros en función del número de kilómetros que recorremos anualmente. (Nota: Necesitas el precio del coche, el del combustible y el consumo combinado).
Lamborguini
precio consumo conbinado precio euro/km Expresión
Gasolina 20.000 5,2 L/100km 1,235 5,2x1,235/100=0,06422 y=20.000+0,064*x
Diesel 23.500 4,4L/100kM 1,009 4,4x1,009/100=0,04439 y=23.500+0,044*x
14.Interpreta la gráfica del recorrido del Maratón Popular de Madrid
15. Explora el uso del programa SURFER en imaginary
AYUDA para incluir applet de GEOGEBRATUBE en tu blog:
1) Incluir el código:
<iframe height="566" width="581" scrolling="no"src="https://tube.geogebra.org/material/iframe/id/190104/width/581/height/566/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/preferhtml5"style="border: 0px currentColor;" ></iframe>
2) Cambiar el enlace en ROJO por nueva url.
3) Cambiando los valores de height y width se ajusta el tamaño.